Ce document a pour but de présenter les bases du fonctionnement des Geometry Nodes, afin de permettre à des débutants de commencer des projets simples. Vous pouvez télécharger une version pdf de cette page ici .

Pour commencer, il faut installer le logiciel Blender : https://www.blender.org/download/.
Dans le cadre du concours, la version qui nous intéresse est la 4.2, qui bénéficie des derniers noeuds de geométrie, ainsi que d'un Long Term Support.

Principes de Base

Que sont les Blender Geometry Nodes ?
Il s'agit d'un outil nodal de géométrie procédurale. Il permet de créer des procédures agissant sur les données de géométrie d’un objet qui sont stockées sous forme de buffers d’attributs.

Géométrie entrante/sortante
Partons du fichier de base blender (le default cube), et ajoutons un geometry node.

Comme on peut le voir sur l'image ci-dessus, le geometry node par défaut contient deux noeuds : la géométrie d’entrée (ici une géométrie de cube), et la géométrie en sortie (évaluée pour le rendu). Bien sûr, si on ne fait rien, les deux noeuds entrée/sortie sont connectés et la géométrie passée en sortie est exactement la même que celle donnée en entrée.

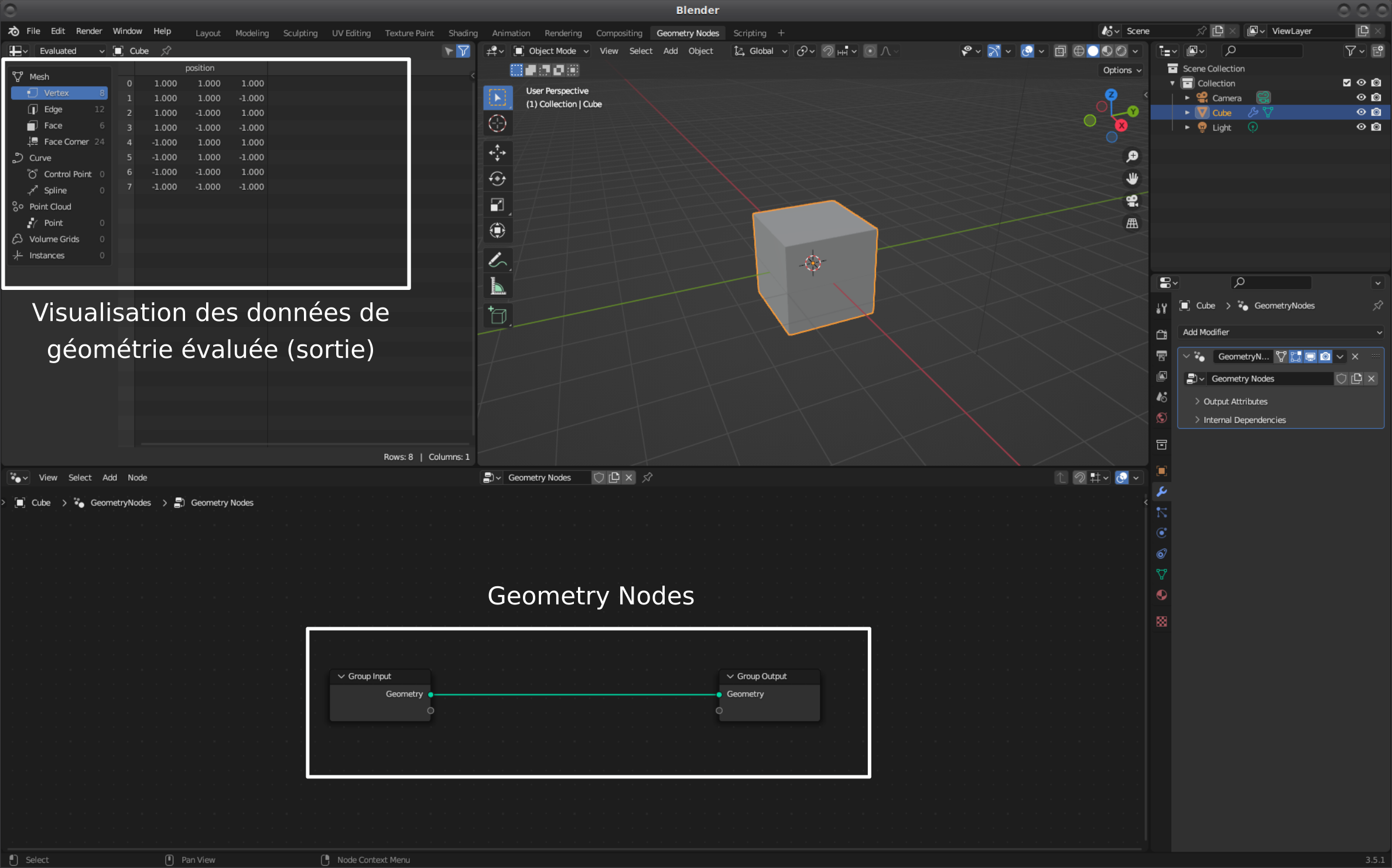
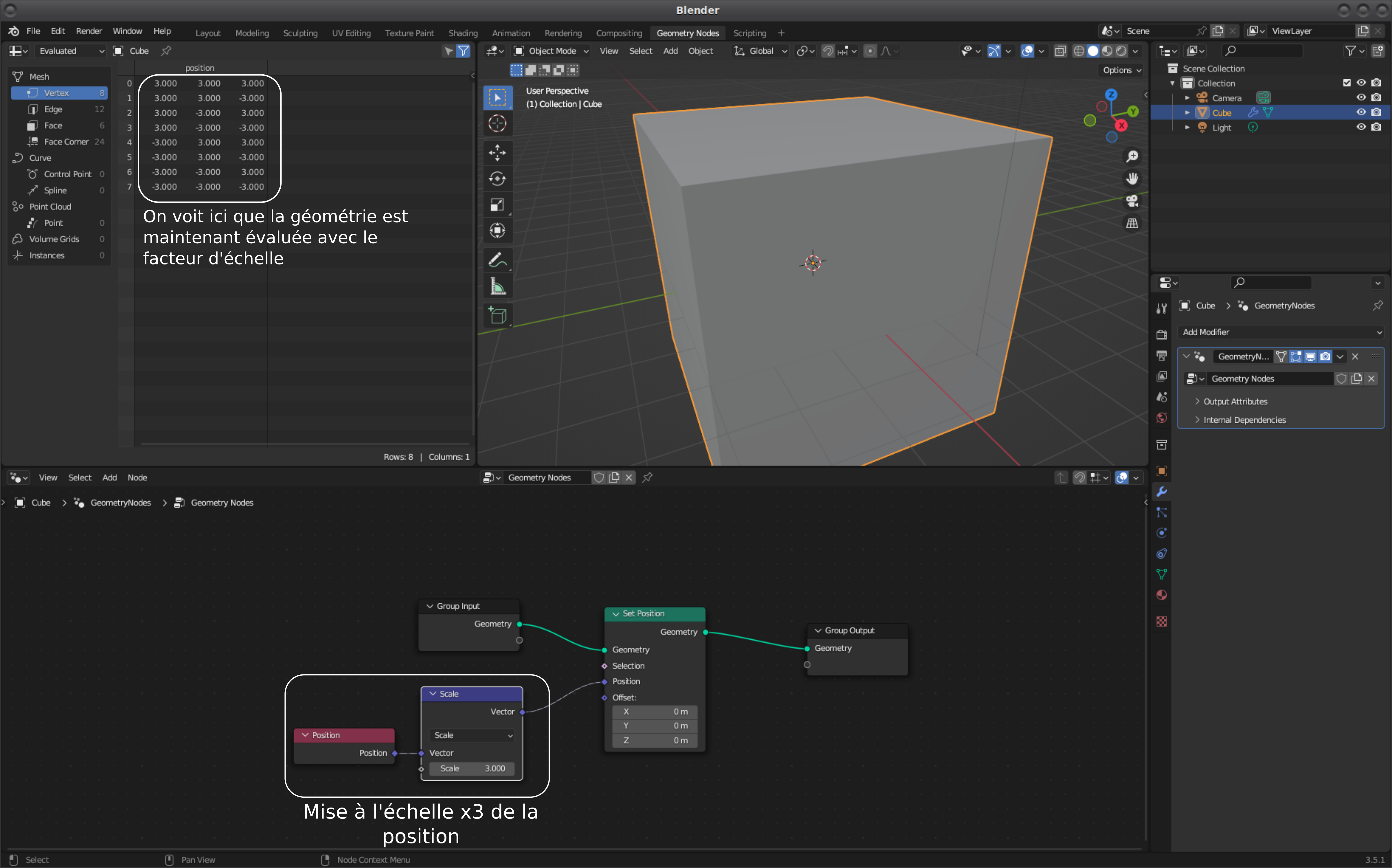
L'idée est donc d'ajouter des noeuds entre les deux pour agir sur la géométrie en entrée. Un exemple simple est montré sur l'image suivante: la mise à l’échelle x3 des coordonnées.

A noter que ce geometry node peut ensuite être réutilisé sur n’importe quel autre objet, il effectuera la même mise à l’échelle sur ses coordonnées de géométrie.

On peut aussi décider de ne pas du tout utiliser l’entrée, et par exemple utiliser une primitive géométrique parmi celles existantes, comme sur l'exemple de l'image suivante.

Quel type de géométrie peut-on traiter ?
Maillages, courbes, nuages de points. Sachant qu’il existe des noeuds qui convertissent certains types en d'autres, de manière plus ou moins directe.

Attributs
Les données de géométrie qu’on manipule sont appelés des attributs, et ils se comportent comme des vertex buffer. Chaque type de géométrie a des attributs de base auxquels on peut accéder. Ces attributs appartiennent à des domaines.

Par exemple dans un maillage, on a l’attribut position qui est défini dans le domaine des vertex, c'est-à-dire que chaque sommet possède une valeur de position dans la géométrie. L’attribut normal est lui défini dans le domaine des faces (une normale par face).
Pour un objet de type curves, on a l’attribut de curve type dans le domaine des splines, et la position dans le domaine des control points.

Nous pouvons aussi calculer de nouveaux attributs à la volée, et éventuellement les enregistrer dans la géométrie pour les ré-utiliser ailleurs (dans le shader node par exemple).

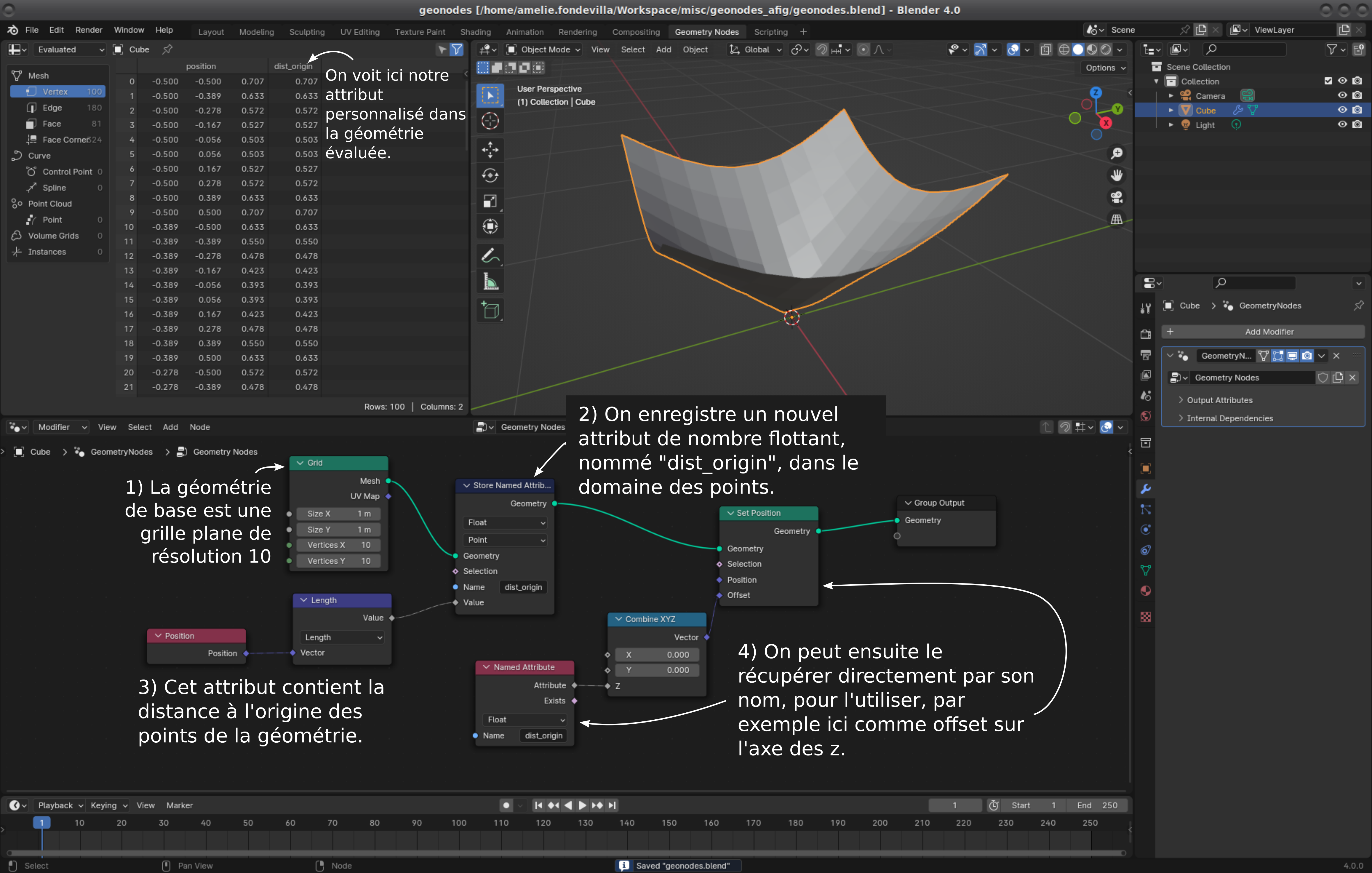
Dans l’exemple de l'image ci-dessus, on a ajouté un nouvel attribut dans la géométrie : dist_origin, qui mesure la distance à l’origine de chacun des vertex, puis on a utilisé cet attribut afin de positionner en hauteur les sommets de la géométrie.

Instances
Il est possible de créer de multiples instances d’une même géométrie, c'est-à-dire plusieurs entités qui partagent les mêmes données de géométrie, mais des matrices de transformation différentes.

Un exemple simple est représenté sur l'image ci-dessus: on positionne des cylindres sur les sommets d’un cube, alignés avec la normale au sommet.
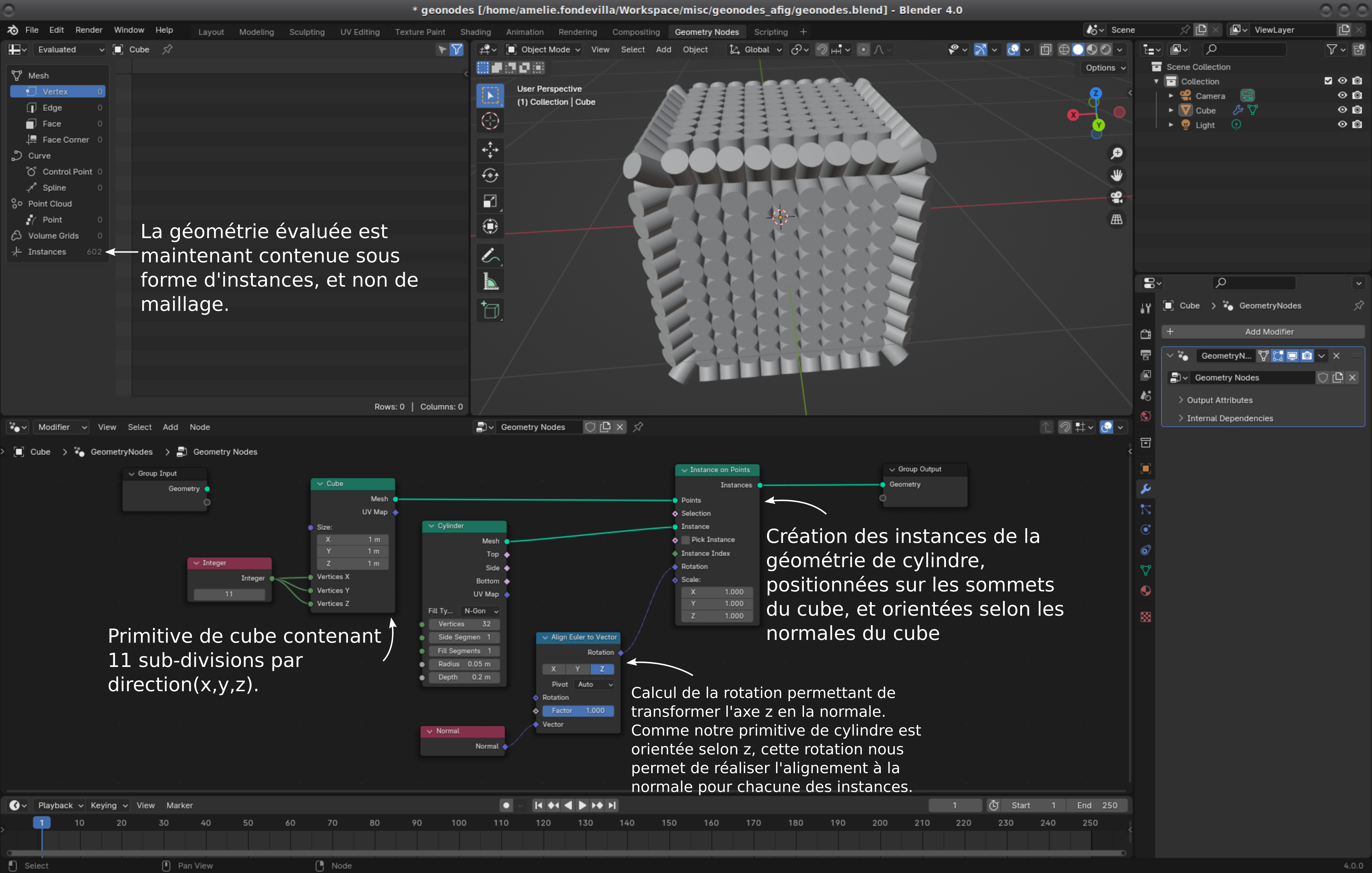
NB: nous avons subdivisé le maillage de cube pour augmenter le nombre de sommets qu'il contient.

Exemples d'application

Nous avons ici compilé un ensemble d’exemples assez variés, et qui touchent de près ou de loin à des thèmes récurrents de la recherche en modélisation géométrique. Bien sûr, le choix de cet échantillon est loin d'être exhaustif, il ne faut pas hésiter à le compléter par une exploration de ce qui se fait, notamment sur internet.

A noter que nous avons réalisé certains exemples (les plus simples!) dans un fichier blender que vous pouvez télécharger ici ils sont indiqués dans ce document par une astérisque *. Les exemples plus complexes sont issus de vidéos youtube indiquées en référence des images.

Modèles récursifs
Il n'existe pas de systèmes de récursivité en tant que tel dans les geometry nodes, mais il est possible de créer des groupes de noeuds (qui se comportent comme des fonctions), et itérer dessus. Ceci permet l’implémentation itérative de modèles récursifs plus ou moins structurés.

Par exemple certaines fractales, de type flocon de Koch en 3D, ou brocoli, comme sur l'image ci-dessous.

Nous pouvons aussi traiter des modèles plus poussés de géométrie procédurale, comme par exemple les bien connus L-systemes pour la création d’arbres et de plantes (voir image ci-dessous). Les fleurs sont aussi des sujets typiques que l’on peut créer facilement à partir d’un seul élément de maillage (pétale) et quelques règles de répartition.

Ces modèles génératifs peuvent aussi être animés de manière procédurale, comme sur l’exemple de cette vidéo d'Entagma.

Modèles de terrain
Un autre type de travail peut porter sur la génération de terrain. Les geometry nodes intègrent des modèles de bruit, qui peuvent être utilisés comme carte de hauteur. On peut aussi complexifier le modèle en définissant des zones de foret, de roches, etc… L’utilisation des attributs sur la géométrie peut alors s’avérer très efficace.

Un exemple très minimal est montré sur l'image ci-dessus, avec et sans matériaux. Bien sûr, on peut pousser ce principe bien plus loin (voir cet exemple plus complet par BlenderDude).

Modèles génératifs à partir d’une géométrie existante
Jusqu’ici, nous nous sommes intéressés uniquement à des exemples dans lesquels la géométrie d’entrée était peu ou pas utilisée. Il existe une autre pan de la géométrie procédurale qui s’adapte à la géométrie d’entrée. Une partie de ces modèles va utiliser comme entrée un ensemble de courbes 3D, et sortir un panel de géométrie stylisée, comme par exemple la corde et les rails illustrés sur l'image suivante.

D’autre part, on peut aussi penser à des modèles de texture 3D avancés. Par exemple les mailles de type tricot, comme sur l'image suivante.

Mais encore
La liste proposée est loin d’être exhaustive. En vrac, quelques autres utilisations de ce système :

• Modélisation de virus en 3D, par Brady Johnston
• Systèmes de particules, par Photini By Design.

On pourra aussi regarder la présentation de Simon Thommes à la Blender Conférence de 2022, intitulée “We can do that with geometry nodes..”. Pour information, Simon Thommes, est artiste chez Blender, spécialisé dans les modèles procéduraux, et travaille en proche collaboration avec les développeurs des geometry nodes.